In this tutorial we can learn about implement the Searching of given number in an one dimensional Array using Linear search and Binary search method:-
Searching:-
Searching is the process to find the given key element in the list with it's position. The Searching is also referred as the locate operation.
Types of Searching is as follows.
1). Linear search method / sequential
search.
search.
2). Binary search method.
Stepwise Procedure:
1) Linear search method:-
In the Linear Searching method,the elements in the list are scanned from the first element till either the required key element is found or the list is over. The key element is compared with every element. This is also called as sequence search method. The list elements are not required to be in specific order. The advantage of the method is its simplicity. But it is efficient only for small sized lists. The maximum iterations required will be the size of the list N.
Pictorial discription:-
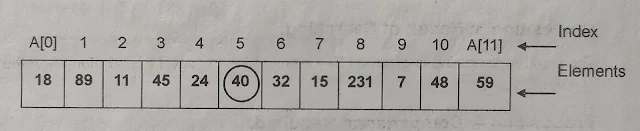
Let us consider a list of Integer elements with N=12 as:
1. If search Key is 40 :
Starting with index = 0, the current element is compared with Key. The Key 40 is found at index position 5. This is depicted pictorially as below:
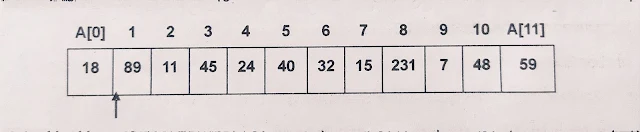
Current element A[0] i.e. 10 ≠ 40, go to next element.
Current element A[1] i.e. 89 ≠ 40, go to next element
Current element A[2], 11 ≠ 40, go to next element
Current element A[3], 45 ≠ 40, go to next element
Current element A[5], 40 = 40, Key Found
Thus Key 40 found at position 5
The result of the linear search as:
- The Key element 40 is Found in Found in the list at position 5.
- The number of comparisons required = 6.
Algorithm:-
1) Start
2) Read element and stored in Array a[ ]
3) Read value of Key to be searched
4) i = 0
5) if (a[ i ] = = Key )
Displayed Record found at location go to step 9
6) i = i++
7) if i < n [ go to step 5]
8) display no match found
9) stop
Program for Linear Searching:-
#include<stdio.h> #include<conio.h>. void main ( )
{
int a[5], i,key, n, flag = 0;
printf("enter no of elements"); scanf("%d",&n);
printf("enter element you want to search"); scanf("enter array element \n"); for( i=0; i<n; i++ ); { scanf("%d",&a[ i ] ); } printf(" Enter element you want to search"); scanf("%d",&key); for( i = 0; i<n; i++ ) { if (a[ i ] = key ) { flag = 1; break; }
} if( flag = 0 ) { printf(" element is not found"); } else { printf(" element is found "); } getch ( );
}
OUTPUT :
enter no of elements 5
enter array elements
5
7
4
3
9
Enter element you want to search 4
element is found
In the binary search method the Key element is compared with the middle element of the list. If they are equal, the search is successful.
Starting with complete list, at particular instance, binary search will use part of the list for searching.
If the middle element is greater than the key, the search process is repeated with the lower half of the list; otherwise the process is repeated with the upper half of the list. Thus every time the comparison is made, the number of the element at yet to be searched are reduced by half.
The search is terminated when either the key element is found or the remaining list to be search has only one element.
As the list is divided into two equal parts for searching the method is called the binary search.
The efficiency of the searching method can be improved by using the sorted list. This Will be reduced the searching time.
Pictorial representation :-
Consider the ascending ordered list for N = 12 number as list.
1. Key to be searched = 35
a) iteration 1: initial index Low = 0 and end index High = 11 for the list to be searched.
Find index of middle element as: Middle =( Low + High ) / 2=5 { Integer result only } The middle position element of the current list is : List[Middle] = List [5] = 50.
As List [5] i.e. 50 is greater than the key element 35, the lower half of the list should be used for the next iteration of the search. To do this current High is modified as High =Middle -1 = 4. First iteration is complete. Go for next iteration with modified search list with Low = 0, High = 4.
b). iteration 2: calculate the new Middle = ( Low + High ) / 2 = ( 0+4 ) / 2= 2.
The Lis[ Middle] = List [2] = 21 is smaller than the Key, so select the upper half of the current list. To do this the Low is modified as Low= Middle + 1= 2+1= 3.
Second iteration is complete.
c) iteration 3: Calculate the new Middle=( Low + High) / 2= ( 3+4 ) / 2 = 3.
The List [ Middle] = List [ 3] = 35 is equal to Key, the Key is found at index = Middle = 3. The number of comparisons required = number of iterations = 3.
Note, the search is continued until the Key does not match the element at Middle position or the list to be searched has one or no elements.
Algorithm:
1). Start
2). Read element and Stored in Array a[ ]
3). Read value of Key to be searched
4). Low = 0. & High = n - 1
5). Middle = High + Low / 2
6). If ( Key = = a[ Middle] )
7). If [ Key < a[ Middle ] ]
High = Middle - 1
else
Low = Middle + 1
8). If ( Low < = High )
9). If ( flag = = 1 )
Element is found
else
Element is not found
10). Stop
Spedo code for binary search:-
#inclide<stdio.h>
#include<conio.h>
void main ( )
{
int a[10] , n, i, Key, flag=0;
int Low=0,mid,high;
printf (" enter no. of elements");
scanf(" %d ", & n );
for( i= 0; i<n; i++ )
{
scanf( " %d", & a[ i ] );
}
printf (" enter element you want to search");
scanf( " %d ", &Key );
High = n - 1;.
do
{
mid = ( Low + High );
if ( a[ mid ] = = Key );.
{
flag = 1;
break;
}
if ( a[mid ]> Key )
{
High = mid -1;
}
else
{
Low = mid +1;
} }
while ( Low<= High )
if ( flag = = 1 )
{
printf ( " element is found ");
}
else
{
printf ( " element is found ");
}
getch( );
}
OUTPUT:-
Enter no.of element
5
1
2
3
4
6
Enter element you want to search 3
Element is found.
} if( flag = 0 ) { printf(" element is not found"); } else { printf(" element is found "); } getch ( );
}
OUTPUT :
enter no of elements 5
enter array elements
5
7
4
3
9
Enter element you want to search 4
element is found
2) Binary search method:-
In the binary search method the Key element is compared with the middle element of the list. If they are equal, the search is successful.
Starting with complete list, at particular instance, binary search will use part of the list for searching.
If the middle element is greater than the key, the search process is repeated with the lower half of the list; otherwise the process is repeated with the upper half of the list. Thus every time the comparison is made, the number of the element at yet to be searched are reduced by half.
The search is terminated when either the key element is found or the remaining list to be search has only one element.
As the list is divided into two equal parts for searching the method is called the binary search.
The efficiency of the searching method can be improved by using the sorted list. This Will be reduced the searching time.
Pictorial representation :-
Consider the ascending ordered list for N = 12 number as list.
1. Key to be searched = 35
a) iteration 1: initial index Low = 0 and end index High = 11 for the list to be searched.
Find index of middle element as: Middle =( Low + High ) / 2=5 { Integer result only } The middle position element of the current list is : List[Middle] = List [5] = 50.
As List [5] i.e. 50 is greater than the key element 35, the lower half of the list should be used for the next iteration of the search. To do this current High is modified as High =Middle -1 = 4. First iteration is complete. Go for next iteration with modified search list with Low = 0, High = 4.
b). iteration 2: calculate the new Middle = ( Low + High ) / 2 = ( 0+4 ) / 2= 2.
The Lis[ Middle] = List [2] = 21 is smaller than the Key, so select the upper half of the current list. To do this the Low is modified as Low= Middle + 1= 2+1= 3.
Second iteration is complete.
c) iteration 3: Calculate the new Middle=( Low + High) / 2= ( 3+4 ) / 2 = 3.
The List [ Middle] = List [ 3] = 35 is equal to Key, the Key is found at index = Middle = 3. The number of comparisons required = number of iterations = 3.
Note, the search is continued until the Key does not match the element at Middle position or the list to be searched has one or no elements.
Algorithm:
1). Start
2). Read element and Stored in Array a[ ]
3). Read value of Key to be searched
4). Low = 0. & High = n - 1
5). Middle = High + Low / 2
6). If ( Key = = a[ Middle] )
7). If [ Key < a[ Middle ] ]
High = Middle - 1
else
Low = Middle + 1
8). If ( Low < = High )
9). If ( flag = = 1 )
Element is found
else
Element is not found
10). Stop
Spedo code for binary search:-
#inclide<stdio.h>
#include<conio.h>
void main ( )
{
int a[10] , n, i, Key, flag=0;
int Low=0,mid,high;
printf (" enter no. of elements");
scanf(" %d ", & n );
for( i= 0; i<n; i++ )
{
scanf( " %d", & a[ i ] );
}
printf (" enter element you want to search");
scanf( " %d ", &Key );
High = n - 1;.
do
{
mid = ( Low + High );
if ( a[ mid ] = = Key );.
{
flag = 1;
break;
}
if ( a[mid ]> Key )
{
High = mid -1;
}
else
{
Low = mid +1;
} }
while ( Low<= High )
if ( flag = = 1 )
{
printf ( " element is found ");
}
else
{
printf ( " element is found ");
}
getch( );
}
OUTPUT:-
Enter no.of element
5
1
2
3
4
6
Enter element you want to search 3
Element is found.












0 Comments