Asymptotic Analysis
You know that data structure is a way to organize data efficiently and that efficiency is measured in terms of time or space. So, an ideal data structure is a structure that takes the least amount of time to perform all its operations and memory space. Our focus will be on finding the complexity of time rather than the complexity of space, and by finding the complexity of time, we can decide which data structure is best for the algorithm.
How to find the Time Complexity or running time for performing the operations?
Measuring actual running time is not at all practical. The running time for any operation depends on the size of the input. Let us understand this statement with a simple example.
Suppose you have an array of 10 elements and you want to add a new element to the begging of the array. To achieve this, you have to move each element to the right, and suppose each element takes time. There are 10 components, so 10 units of time will be taken. Suppose an array has 1000 components, then it takes 1000 units to shift. It concludes that the complexity of time depends on the input size.
if the input size is n, then f(n) is a function of n that denotes the time complexity.
The time required for the algorithm is calculated in three ways:
Worst case: It defines the input for which the algorithm takes a long time.
Average case: It takes average time for the program execution.
Best case: It defines the input for which the algorithm takes the lowest time
Asymptotic Notations
The following are some commonly used asymptomatic notations used to calculate algorithm running time complexity:
- Big oh Notation (?)
- Omega Notation (Ω)
- Theta Notation (θ)
Big oh Notation (O)
- Big O notation is an asymptomatic notation that measures the efficiency of an algorithm by sequencing the growth of a function.
- This notation provides an upper bound to the function which ensures that the function never grows faster than the upper bound. Therefore, it gives a minimum upper bound to the function so that the function cannot grow faster than this upper bound.
The algorithm is a formal way of expressing the upper limit of current time. It measures the worst state of time complexity or the longest time to complete the operation of an algorithm. It is presented as shown below:
diagram
For example:
If f(n) and g(n) are the two functions defined for positive integers,
then f(n) = O(g(n)) as f(n) is big oh of g(n) or f(n) is on the order of g(n)) if there exists constants c and no such that:
f(n)≤c.g(n) for all n≥no
This indicates that f (n) does not grow faster than g (n) or g (n) is the upper limit on the function f (n). In this case, we are measuring the growth rate of the function which ultimately calculates the worst time complexity of the function, i.e., how badly the algorithm can perform.
Omega Notation (Ω)
- It basically describes the best situation which is the opposite of Big O notation.
- This is a formal way to show the lower limit of the running time of the algorithm. This algorithm calculates the complexity of the best time or best-case time to complete.
- It determines the fastest time the algorithm can run.
If we need the algorithm to take at least some time without using the upper bound, we use the big- Ω notation, i.e. the Greek letter "omega". It is used to bind the increase in running time for large input sizes.
If f(n) and g(n) are the two functions defined for positive integers,
then f(n) = Ω (g(n)) as f(n) is Omega of g(n) or f(n) is on the order of g(n)) if there exists constants c and no such that:
f(n)>=c.g(n) for all n≥no and c>0
Theta Notation (θ)
- Theta notation mainly describes the average case scenario.
- This shows the real time complexity of the algorithm. Each time, the algorithm does not perform the worst or the best, in real-world issues, the algorithms mainly fluctuate between the worst-case and the best-case, and this gives us the average case of the algorithm.
- Big Theta is mainly used when the value of worst-case and best-case is the same.
- The algorithm is a formal way of expressing both upper bound and lower bound of running time.
Let's understand the big theta notation mathematically:
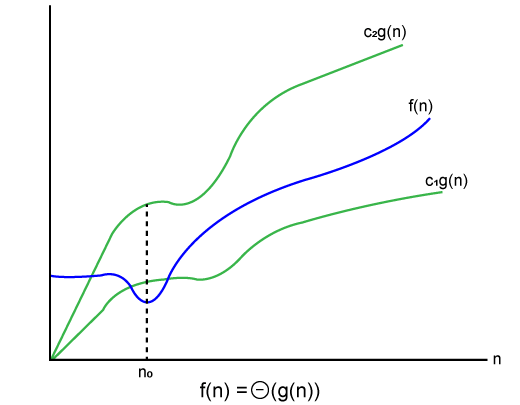
Let f(n) and g(n) be the functions of n where n is the steps required to execute the program then:
f(n)= θg(n)
The above condition is satisfied only if when
c1.g(n)<=f(n)<=c2.g(n)
Where the function is bounded by two limits, i.e., upper and lower limits, and f (n). The condition f (n) = θg (n) is true if and only if c1.g (n) is less than or equal to f (n) and c2.g (n) is greater than or equal to f (n). The graphical representation of theta notation is given below:
Topics :





0 Comments